NCEMSS - a program for simulation of HRTEM images
1. Introduction to the simulation process
1.1 Why simulate images ?
Image simulation grew out of an attempt to explain why electron microscope
images of complex oxides sometimes showed black dots in patterns corresponding
to the patterns of heavy metal sites in complex oxides, and yet other images
sometimes showed white dots in the same patterns. This first application was
therefore to characterize the experimental images, that is to relate the
image character (the patterns of light and dark dots) to known features in
the structure.
Most simulations today are carried out for similar reasons, or even as a
means of structure determination. Given a number of possible models for the
structure under investigation, images are simulated from these models and
compared with experimental images obtained on a high-resolution electron microscope.
In this way, some of the postulated models can be ruled out until only one
remains. If all possible models have been examined, then the remaining model
is the correct one for the structure. For this process to produce a correct
result, the investigator must ensure that all possible models have been examined,
and compared with experimental images over a wide range of crystal thickness
and microscope defocus. It is also a good idea to match simulations and experimental
images for more than one orientation.
Some simulations are done in order to throughly explore one particular image
by “freeze-framing” the imaging process in the computer. In this way, we can
obtain information that is not observable experimentally, such as the electron
wave amplitude at the exit surface of the specimen, the magnitude and phase
of each component of the image intensity spectrum, or even the amplitude
contributed to the intensity spectrum by each pair of diffracted-beam interferences.
The simulation programs can also be used to study the imaging process itself.
By simulating images for imaginary electron microscopes, we can look for ways
in which to improve the performance of present-day instruments, or even find
that the performance of an existing electron microscope can be improved significantly
by minor changes in some instrumental parameter. Alternatively, based on
imaging requirements revealed by test simulations, we can adjust the electron
microscope to produce suitable images of some particular specimen, or even
of some particular feature in a particular specimen.
1.2 Describing the transmission electron microscope
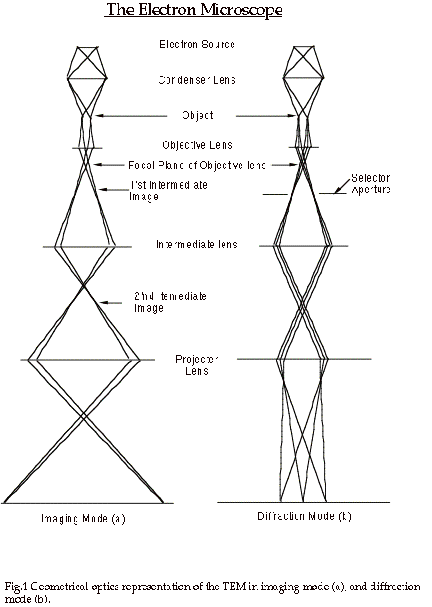
In order to simulate an electron microscope image, we need firstly to be able to describe the electron microscope in such a way that we can model the manner in which it produces the image. As a first step, we can consider the usual geometrical optics depiction of the transmission electron microscope (TEM).
Figure 1 shows such a diagram of a TEM operated in two distinct modes, set
up for microscopy (a), and for diffraction (b). In microscopy mode we see
that the TEM consists of an electron source producing a beam of electrons
that are focused by a condenser lens onto the specimen; electrons passing
through the specimen are focused by the objective lens to form an image called
the first intermediate image (I1); this first intermediate image forms the
“object” for the next lens, the intermediate lens, which produces a magnified
image of it called the second intermediate image (I2); in turn, this second
intermediate image becomes the “object” for the projector lens; the projector
lens forms the greatly-magnified final image on the viewing screen of the
microscope. In microscopy mode, electrons that emerge from the same point
on the specimen exit surface are brought together at the same point in the
final image.
At the focal plane of the objective lens, we see that electrons are brought
together that have left the specimen at different points but at the same angle.
The diffraction pattern that is formed at the focal plane of the objective
lens can be viewed on the viewing screen of the TEM by weakening the intermediate
lens to place the microscope in diffraction mode (b).
1.3 Simplifying the description of the TEM
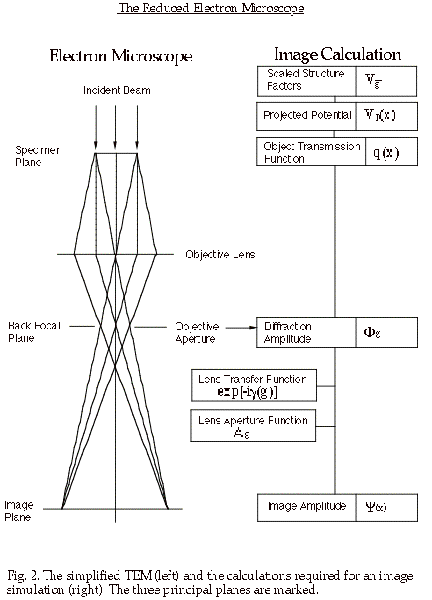
Consideration of the description of the electron microscope in figure 1 shows that the projector lens and the intermediate lens (or lenses) merely magnify the original image (I1) formed by the objective lens. For the purposes of image simulation we can reduce the TEM to three essential components; (1) an electron beam that passes through (2) a specimen, and then through (3) an objective lens (fig.2).
Our next step in describing the electron microscope for image simulation
is to move from the geometrical optics description of the TEM to a description
based on wave optics. In this description of the microscope we examine the
amplitude of the electron wavefield on various planes within the TEM, and
attempt to determine how the wavefield at the viewing screen comes to contain
an image of our specimen.
By treating the electrons as waves, and considering our simplified electron
microscope (fig.2), we see that there are three planes in the TEM at which
we need to be able to compute the (complex) amplitude of the electron wavefield.
(1) The image plane:
Working backwards, we start with our desired information, the electron wavefield
at the image plane; this wavefield is derived from the wavefield at the focal
plane of the objective lens by applying the effects of the objective aperture
and the phase changes introduced by the objective lens.
(2) The focal plane of the objective lens:
In turn, the electron wavefield at the focal plane of the lens is derived
from the wavefield at the exit surface of the specimen by a simple Fourier
transformation.
(3) The specimen exit surface:
In order to know the exit-surface wavefield, we must know with which physical property of the specimen the wave interacts, and describe that physical property for our particular specimen.
Cowley and Moodie (1957) showed that the interaction of an electron beam with a specimen could be described by the so-called multislice approximation, in which electrons propagate through the specimen and scatter from the crystal potential; the electron scattering is described by the so-called phase-grating function, a complex function of the potential, and the electron propagation is computed with a propagation function dependent on the electron wavelength.
1.4 Simulating TEM images
The problem of simulating images thus becomes a problem of computing the electron wavefields at the three microscope planes. Currently, the best way to produce simulated images is to divide the overall calculation into three parts:
(1) Model the specimen structure to find its potential in the direction
of the incident beam.
(2) Produce the exit-surface wavefield by considering the interaction of the incident electron wave on the specimen potential.
(3) Compute the image-plane wavefield by imposing the effects of the objective lens on the specimen exit surface wave.
2. Introduction to NCEMSS
2.1 The three simulation steps
Since the simulation problem divides neatly
into three parts, NCEMSS treats these three parts with three sub-programs
-
(1) PHSGRT - a program to generate the part
of the crystal potential that produces electron scattering; input is from
a file containing structural data about the specimen, including unit cell
dimensions, symmetries, and atom positions, occupancies, and temperature factors.
(2) MSLICE - a program to generate the electron wavefield at the specimen exit surface; it uses PHSGRT data combined with information about the accelerating voltage of the electron microscope, and the specimen thickness and tilt.
(3) IMAGE - a program to generate the image intensity at the microscope
image plane; the effects of objective lens phase changes and resolution-limiting
aberrations are included via parameters like defocus, spherical aberration,
incident beam convergence, spread-of-focus, and the position and size of the
objective aperture
Thus PHSGRT considers only the specimen structure, MSLICE treats the interaction
of the specimen with the electron wave, and IMAGE simulates how the wave leaving
the specimen interacts with the lens system of the electron microscope. Once
a simulation has been made, any additional simulation will usually not require
a full re-simulation; any change in microscope parameters will not affect
the results of the PHSGRT and MSLICE programs, and only IMAGE will need to
be re-run; any change in microscope voltage or in specimen thickness or tilt
will not affect the results of PHSGRT, but MSLICE and IMAGE will need to
be re-run. Of course, any change in the specimen structure will require the
re-running of all three subprograms.
2.2 NCEMSS files
Supplied files: NCEMSS uses four data files to store supplied information not normally altered by the user:
(1) spcgrp.dat stores information on all 230 space groups for generation
of crystal symmetry operators as required by the input specimen structures.
(2) scatt.dat stores information on atomic scattering factors for the first
98 elements.
(3) microscopes.dat stores information on the imaging parameters of various
high-resolution electron microscopes. Note that the user has the option
of adding additional microscopes to the table stored in MICROSCOPES.DAT.
(4) lprint.ps stores a set of Postscript definitions that are used in order to print images to a Postscript Laserprinter.
Generated files: NCEMSS generates and stores various data files in the course
of a simulation. The five data files are:
(1) name.at stores all the structure and microscope information needed to
run the simulation. This information is derived from user input and the supplied
data files. In particular, the string “name” is a unique name for the structure,
input by the user when creating the structure file.
(2) name.pout is the result of running the PHSGRT subprogam from the information
stored in name.at; it contains the specimen potential in the direction of
the electron beam.
(3) name.mout is the result of running the MSLICE subprogram using the data
in name.pout with those in name.at; it contains the exit-surface wave at one
or more selected specimen thicknesses.
(4) name.iout is the result of running the IMAGE subprogram to apply the
effects of the microscope parameters in the name.at file to the exit-surface
wave; it contains one or more images ready to be displayed.
(5) name.aout contains the complex amplitudes of several diffracted beams
at one-slice increments in specimen thickness. The beams are specified by
the user in the main menu, and can be plotted as a function of specimenthickness.
In addition, two print files are produced (but rarely printed) just in case additional information about a computation is required by the user. These files are:
(6) name.p_prnt contains information about the way in which the PHSGRT subprogram processed the name.at data to produce the specimen potential.
(7) name.m_prnt contains information about the way in which the MSLICE subprogram
processed the name.pout data with name.at data to produce the exit-surface
wave; that is, it contains information on the multislice computation.
Since NCEMSS images are stored in a file for interactive display, the user
has the option of writing any image to the display screen with any selected
number of unit cells, with any selected value of contrast and brightness,
and at any selected magnification. In addition, the user may elect to display
(i.e. write to the screen) real-space functions like the projected crystal
potential, the exit-surface electron wavefunction, or a drawing of the atom
positions; in addition, reciprocal-space functions such as the diffraction
intensities and the image power spectrum (“optical” diffractogram) may be
displayed and indexed.
3. Running NCEMSS
Note on Platform dependency:
NCEMSS was originally written for a terminal emulating tektronix 4014 commands.
The menus were written to the terminal and the images were displayed on a
framestore. The code was executing on a Digital Equipment Corporation microVax
II computer under the VMS operating systems. The code has since been ported
to other platforms and will run on DEC VMS and Ultrix workstations and on
various flavors of Unix running X-windows. However, because of the origin
of the program, it still an old style layout dictated by the tektronix terminal.
The program uses two windows. One looking like a graphics window displaying
push-button style menus and one window for displaying graphics output such
as images, diffraction patterns and views of unit cells. The program does
not have a modern style interface with a menubar and pull down menus.
NCEMSS is run interactively at a graphics screen using a mouse or other
pointing device. The graphics screen may be a a workstation console, an X-window
terminal or any computer running as an x-window server. Commands are issued
to NCEMSS by moving a cursor to select an appropriate item from a menu. Sometimes,
selecting an item from a menu will produce another menu with additional options.
Because of constant changes, the menus mentioned in this manual may not
always correspond to the current version of the program for a particular
platform. The text will be appropriate for the UNIX version of the program.
3.1 Getting started
If started from an X-terminal, first type setenv DISPLAY <IP address> to set the output to the X-window terminal.
Start NCEMSS by typing ncemss followed by a carriage return:
ncemss (return)
this action will produce the SINGLE/LAYERED menu, by opening two windows
on the workstation screen, one being the menu (control) window, the other
the image window.
3.2 The SINGLE/LAYERED menu
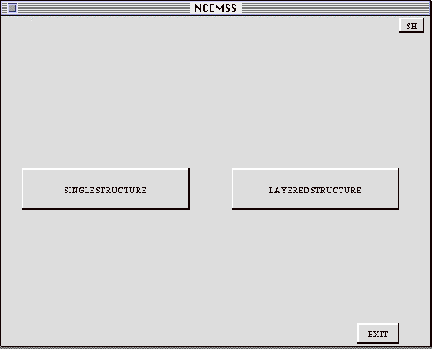
The first menu encountered by the user on starting to work with NCEMSS consists
of three labeled boxes. Any one of these boxes or buttons can be activated
by using the mouse to move the screen cursor into the area of the screen within
the box, and then pressing the LEFT button on the mouse. At the lower right
of the window is the EXIT box, or button. Selecting this box will cause the
program to exit and return to the system prompt.
The two major boxes allow the user to specify a choice of either a SINGLE
STRUCTURE calculation, or a calculation of the images arising from a LAYERED
STRUCTURE. A SINGLE STRUCTURE calculation is one where the specimen structure
repeats regularly in thedirection of the electron beam, and is the usual type
of image simulation. A LAYERED STRUCTURE calculation is a simulation in which
the specimen structure is built up of a number of different structural layers
in the electron beam direction, so that the computation requires the use
of more than one crystal structure file. Selecting the LAYERED STRUCTURE box
produces the SET LAYERS menu. Selecting SINGLE STRUCTURE produces the FILE-LIST
menu.
3.3 The FILE-LIST menu
The FILE-LIST menu lists the user’s structure files on the screen. In addition, there are four boxes across the top of the menu, and three boxes across the bottom. The four top boxes control the listing of the structure names; the right hand pair allow the user to “page” through the list, displaying subsequent pages of structure file names.
The top left boxes can be used to select lists of files from either the
user’s PERSONAL collection of structure files, or from a COMMON collection
available to all users on the system. The files in the COMMON collection
can often serve as useful templates for modification to the user’s needs.
On entry to the FILE-LIST menu, the PERSONAL box is selected automatically.
To obtain the COMMON list, move the cursor to the COMMON box and press the
LEFT button on the mouse. To return to your PERSONAL file collection, move
the cursor to the PERSONAL box and press the button.
The three boxes at the bottom of the menu are used to proceed from the current
menu. The rightmost box is the RETURN box, and is used to go back to the previous
menu. Note that many menus have this facility, with the RETURN box situated
in the bottom right corner of the menu. The bottom left box is used to notify
NCEMSS that the user wishes to use one of the displayed structure files.
Moving the cursor to this USE DISPLAYED FILE box and selecting it by clicking
the mouse button removes all the other boxes, and allows the user to select
one of the displayed files by moving the cursor to the correct filename and
clicking the mouse button. Selecting a structure filename causes NCEMSS to
read the file and display its parameters in the PARAMETER menu (often referred
to as the MAIN or CONTROL menu, because it is the one from which the NCEMSS
computation is controlled by the user). The CONTROL menu.
The CREATE NEW FILE box is selected when the user desires to input a new
structural file. Selecting this box with the cursor causes NCEMSS to ask for
a unique name for the structure. Entry of the name then produces a PARAMETER
menu with no parameter values, and a series of prompts from NCEMSS explaining
each parameter needed for input.
HELP: If this is your first use of NCEMSS, it may be helpful to try moving
the cursor to each box in turn, asking for the HELP facility by clicking the
CENTER button on the mouse as each box is reached. The HELP facility is available
for every command box on every menu, and should provide enough information
that you will need to consult this Guide only infrequently.
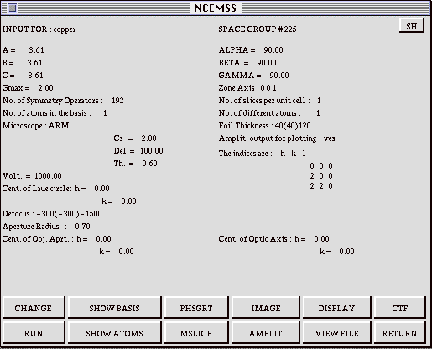
3.4 The PARAMETER or MAIN or CONTROL menu
The main CONTROL menu lists a summary of the control parameters for the current simulation as well as twelve boxes for control of the computation.
When the CREATE NEW FILE option of the FILE-LIST menu is selected, an empty
PARAMETER menu (with no control boxes) is presented, and NCEMSS prompts for
parameters. These parameters have the same form as those presented in the
PARAMETER menu when a structure filename is selected from the FILE-LIST menu.
When every parameter has been entered, NCEMSS re-presents the PARAMETER menu
with the control boxes drawn in and available for use.
3.4.1 Parameters of the PARAMETER menu
INPUT FOR: The parameter displayed next to this prompt is a short title for the structure.
SPACE GROUP #: NCEMSS generates symmetry operators for any one of the 230 space groups, when given the number of the space group required (listed in the International Tables for Crystallography). If the space group required is not one listed in the Tables, a value of zero can be entered.
A, B, C, ALPHA, BETA, GAMMA: These are the unit cell dimensions in Angstrom
units, and the unit cell angles in degrees.
GMAX: The maximum value (in reciprocal Angstrom units) of g to be considered
in the multislice diffraction calculation. This value imposes an “aperture”
on the diffracted beams included in the dynamic scattering process. It should
be large enough to ensure that all significant beam interactions are included.
For light atoms and thin crystals, values as low as 2.0 are adequate. For
structures with heavy atoms and large crystal thicknesses, values of 3.0 to
4.0 are to be preferred. Note that NCEMSS will compute phase-grating coefficients
out to twice GMAX in order to include dynamical interactions correctly (Appendix
A).
ZONE AXIS: Specimen orientation is selected by specifying the zone axis
desired. Three indices are entered with one space between each.
NO. OF SYMMETRY OPERATORS: If a space group has been selected, the correct
value for this parameter will have been entered by NCEMSS. If a value of zero
has been entered for the SPACE GROUP #, then the correct number of operators
must be entered here.
NO. OF SLICES PER UNIT CELL: For unit cells with large repeat distances
in the beam direction, moderate values of GMAX may allow the Ewald sphere
to approach the so-called pseudo-upper-layer line that the multislice allows
at the reciprocal of the chosen slice thickness. In this case NCEMSS will
sub-divide the slice into two or more subslices. How this is done depends
upon the potential setting chosen in the SET-UP menu.
NO. OF ATOMS IN THE BASIS: This value is the number of independent atom positions in the basis or asymmetric unit of the cell. When operated on by the symmetry operators, the basis generates all the atom positions within the cell.
NO. OF DIFFERENT ATOMS: This value is the number of different types of atoms
in the specimen structure; difference is due to a different Debye-Waller factor
or different atomic number.
MICROSCOPE: The type of electron microscope used to generate the imaging
parameters. If a type known to NCEMSS is entered, then NCEMSS provide values
for CS, the spherical aberration coefficient of the objective lens (in mm.);
DEL, the halfwidth of a Gaussian spread of focus due to chromatic aberration
(in Angstrom units); TH., the semi-angle of incident beam convergence (in
milliradian). If the type of microscope is unknown to NCEMSS, the above values
must be entered seperately (or the data file MICROSCOPES.DAT may be edited
to include an appropriate microscope type).
FOIL THICKNESS: The thickness of the specimen foil may be entered as one
single number representing the thickness in Angstrom units, or as a series
of thicknesses represented by the upper and lower bounds and a thickness step;
e.g. 100(50)250 will cause NCEMSS to store the exit wavefield at specimen
thicknesses of 100Å to 250Å in steps of 50Å (a total of four thicknesses).
AMPLIT. OUTPUT FOR PLOTTING: A number of diffracted beams may be selected
for plotting of their intensity and phase variation as a function of specimen
thickness. If YES is answered to the NCEMSS prompt, the number of beams and
their indices may be entered.
VOLT.: The electron microscope accelerating voltage in kilovolts.
CENT. OF LAUE CIRCLE: Specimen tilt is specified by entering the center
of the Laue circle in units of the h and k indices of the projected two-dimensional
reciprocal-space unit cell.
DEFOCUS: The defocus of the objective lens is entered in Ångstrom units
with a negative value representing underfocus (weakening of the lens current).
As for the FOIL THICKNESS parameter, a single value of defocus may be entered,
or a range specified by the upper and lower bounds and the interval; -300(-200)-1100
means defocus values of -300Å, -500Å, -700Å, -900Å and -1100Å.
APERTURE RADIUS: The radius of the objective aperture is specified in reciprocal
Ångstrom units.
CENT. OF OBJ. APRT.: The center of the objective aperture is defined in
units of the h and k indices of the two-dimensional reciprocal-space unit
cell, as for the Laue circle center.
CENT. OF OPTIC AXIS: The center of the optic axis of the electron microscope
is specified in terms of the h and k indices of the two-dimensional reciprocal-space
unit cell, just as for the Laue circle center and the aperture center.
3.4.2 Control boxes
CHANGE: When the CHANGE box is activated by clicking the mouse with the cursor within the CHANGE box boundaries, any parameter value may be changed simply by moving the cursor to the parameter position, clicking the mouse and entering the new value from the keyboard in response to the NCEMSS prompt. To leave CHANGE mode, deactivate the CHANGE box by clicking the mouse with the cursor once again positioned over the CHANGE box.
RUN: Activating the RUN box will cause NCEMSS to run an image simulation
for the current values of the parameters shown in the PARAMETER menu. NCEMSS
will automatically run the least required computation, starting with the PHSGRT
program only if a structure parameter has been changed since the last run
of this data, and starting with the IMAGE program if the only change has
been in the electron microscope imaging parameters.
SHOW BASIS: This box will cause NCEMSS to display the BASIS menu, a list
of the atom positions making up the basis.
SHOW ATOMS: this box will cause NCEMSS to display the ATOM-LIST menu, a
list of all the atom positions in the unit cell.
PHSGRT: Activating the PHSGRT control box will run the PHSGRT sub-program
for the current parameter values.
MSLICE: Activating the MSLICE control box will run the MSLICE sub-program
for the current parameter values.
IMAGE: Activating the IMAGE control box will run the IMAGE sub-program for
the current parameter values.
AMPLIT: Activating the AMPLIT control box will open up a plotting window,
and ask the user which of the stored diffracted beam amplitudes to plot (assuming
that some diffracted beams were stored by specifying their indices before
the MSLICE was run).
DISPLAY: This control box is used to activate the IMAGE-DISPLAY menu for
writing images to the display screen.
VIEW FILE: Activating this control box causes NCEMSS to ask which print
file to display, then to display it.
CTF: Activating this control box produces a linear-image Contrast Transfer
Function under the imaging conditions specified by the current parameter values.
RETURN: Return to previous FILE-LIST menu.
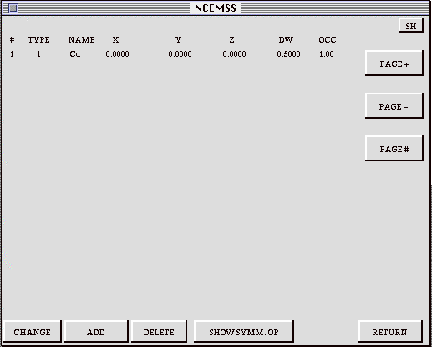
3.5 The BASIS menu
The BASIS menu shows a list of the atom positions making up the basis; when operated upon by the symmetry operators, the basisyields the full set of unit cell atom positions. The BASIS menu displays the atom positions, showing the chemical symbol (NAME) for each atom, its fractional coordinates (X,Y,Z), the Debye-Waller factor, and the site occupancy. Subsequent pages of long lists can be viewed with the three right-hand control boxes.
CHANGE: The value of any parameter can be changed by activating the CHANGE
box, then moving the cursor to the parameter position, clicking the mouse
and entering the replacement value.
ADD: Additional atom positions may be added by activating the ADD box and
entering parameter values in response to prompts.
DELETE: Activating the DELETE box, then moving the cursor to the appropriate
line, will delete the line.
SHOW SYMM. OP: A list of the symmetry operators may be obtained by activating
this control box in order to bring up the SYMM-OP menu.
RETURN: Return to previous MAIN menu.
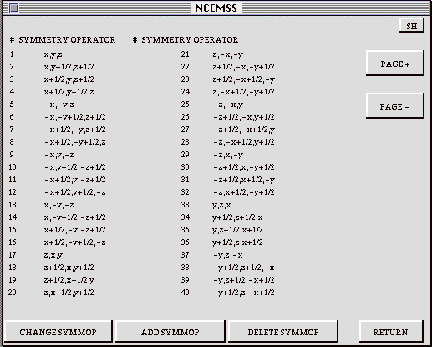
3.6 The SYMM-OP menu
The SYMM-OP menu shows a list of the symmetry operators generated by the
chosen space group (or input by the user when a space group number of zero
is entered in the MAIN menu. The right-hand control boxes are used to page
through long lists of symmetry operators.
CHANGE: Any operator may be replaced by activating the CHANGE box, clicking
the mouse over the appropriate line, and entering the new operator.
ADD SYMMOP: Activating this control box enables the user to add a new operator
to the list.
DELETE SYMMOP: Activating this box, then placing the cursor over any operator
and clicking the mouse, will delete that operator.
RETURN: Return to previous BASIS menu.
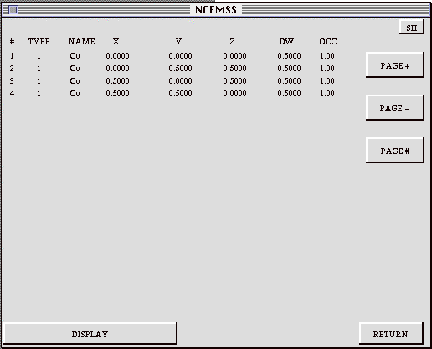
3.7 The ATOM-LIST menu
The ATOM-LIST menu shows a list of the atom positions making up the unit
cell. The list displays the atom positions one per line, showing the chemical
symbol (NAME) for each atom, its fractional coordinates (X,Y,Z), the Debye-Waller
factor (DW), and the site occupancy (OCC). Subsequent pages of long lists
of atom position parameters can be viewed with the three right-hand control
boxes.
BUILD CELL (not implemented on Unix Versions): Activating the BUILD control
box brings up the BUILD menu with the facility of generating defect cells.
DISPLAY: Activating this control box brings up the ATOM-DISPLAY menu, for
the purpose of drawing an atom model of the current structure.
RETURN: Return to previous MAIN menu.
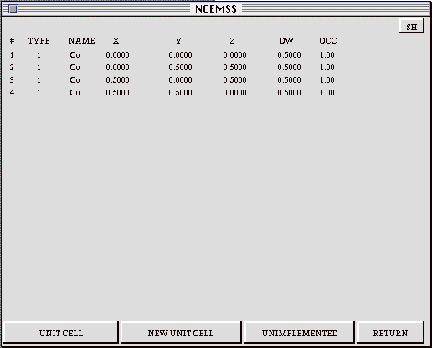
3.8 The ATOM-DISPLAY menu
When DISPLAY is selected in the ATOM-LIST menu, most of the control buttons are replaced to produce the ATOM-DISPLAY menu. The ATOM-DISPLAY menu has only four control boxes.
UNIT CELL: Activating this box splits it in two. Selecting either option
causes NCEMSS to ask for the viewing direction indices to be input from the
keyboard; NCEMSS then draws the unit cell, either with or without perspective.
NEW UNIT CELL: As for UNIT CELL, but for drawing any new unit cell produced
with the BUILD menu.
3-D ATOM DISPLAY: This control box initiates a three-dimensional atom drawing
routine based on a routine written by W.O. Saxton. It can be used to produce
publication-quality atom model drawings with a wide range of different lighting
conditions. This procedure is not implemented on most versions of NCEMSS,
specifically all unix version
RETURN: Return to previous ATOM-LIST menu.
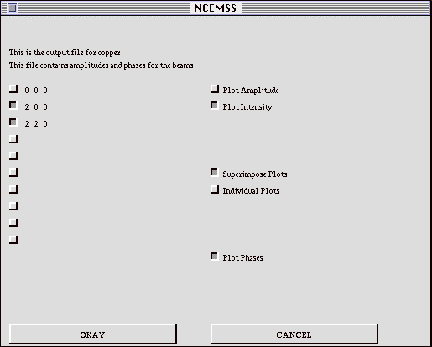
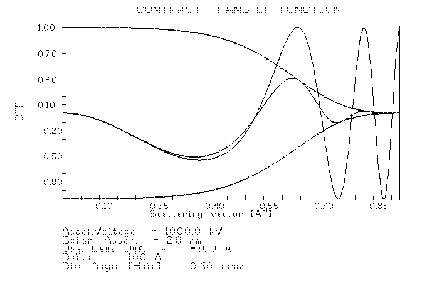
3.9 The AMPLIT menu
On activating the AMPLIT control box on the MAIN menu, the user will be
presented with a list of the diffracted beams for which the complex amplitudes
are currently stored as a function of specimen thickness. NCEMSS will ask
the user to select which beams to plot, whether to superimpose the plots,
and whether to include phase plots. The plots will be drawn with thickness
horizontal and marked in Angstrom units. The various curves can be marked
with the appropriate beam indices by using the TEXT option of the SET-UP
menu.
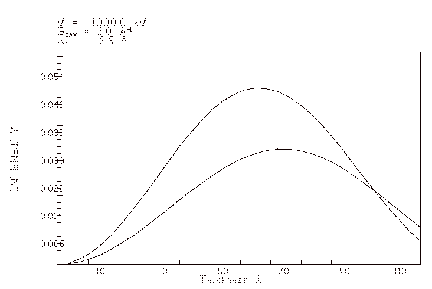
3.10 The CTF plot
The result of activating the CTF control button on the MAIN menu is a plot of the linear-image Contrast Transfer Function. This function is first plotted as the undamped sine part of the complex phase change due to the objective lens spherical aberration and defocus. The damping curves due to the effects of spatial and temporal coherence (incident beam convergence and spread of defocus) are plotted next, then finally the result of imposing the damping on the sine curve. Remember that this curve is only useful for estimating the linear contribution to the image of the diffracted beams exiting a thin crystal (one in which they have suffered only essentially kinematic scattering).
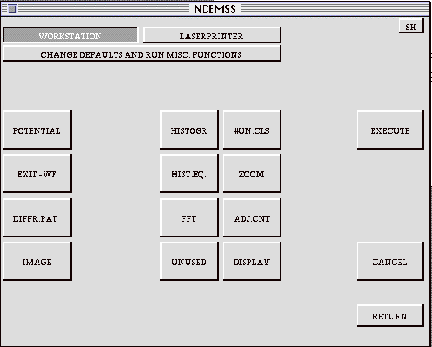
3.11 The IMAGE-DISPLAY menu
When DISPLAY is selected in the MAIN or CONTROL menu, NCEMSS brings up the IMAGE-DISPLAY menu. This menu consists of 21 control buttons. The top three are used to select various options that remain until reset. The left-hand column is used to select the function to be displayed. Other control boxes select the actions to be taken.
WORKSTATION/LASERPRINTER: These two boxes are mutually exclusive and are
used to select the output device for the image display.
CHANGE DEFAULTS AND RUN MISC. FUNCTIONS: This control is used to bring up
the SET-UP menu where various imaging options and defaults may be set.
POTENTIAL: Selecting this input produces a display of the unit cell potential
projected in the incident electron beam direction.
EXIT-WF: The electron wavefield at the crystal exit surface may be displayed
by selecting this input function.
DIFFR.PAT.: Selects the diffraction pattern for display.
IMAGE: Selects the current image for display.
HISTOGR: Produces a histogram of the intensity values in the function selected
from column one.
HIST.EQ.: Stretches the image contrast by performing a histogram equalization
operation before display.
ADJ.CNT: Brings up the SET-CONTRAST menu for selection of contrast parameters
before display.
FFT: Performs a fast Fourier transform on the selected function and squares
the result before display. (Performed on the image, FFT produces the image
power spectrum or “optical diffractogram”).
#UN.CLS: Enables input of the number of unit cells desired in the displayed
image.
ZOOM: Asks for a factor to use in magnification the image.
DISPLAY: Directs the output to the display device.
EXECUTE: Takes the selected function, applies the selected operations, and
outputs the picture.
CANCEL: Cancels the selected options, usually because one was selected by
mistake.
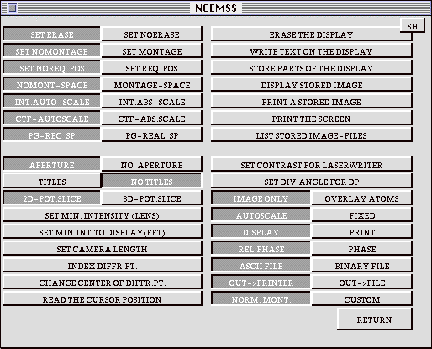
3.12 The SET-UP menu
Opting to change the various defaults by selecting the CHANGE box in the IMAGE-DISPLAY menu, brings up the SET-UP menu. This menu is used to change the default settings of some “hard” parameters, and to manipulate the image display. The nine two-way switches on the left of the menu are normally set to default to the left-hand setting.
SET ERASE<>NOERASE: When ERASE is set, the display screen will be
erased before each new image is displayed (except see MONTAGE).
SET NOMONTAGE<>MONTAGE: When NOMONTAGE is set, only one image will
be displayed for each activation of the EXECUTE command from the IMAGE-DISPLAY
menu. When MONTAGE is set, then a full through-thickness and/or through-focus
series of images will be displayed at one EXECUTE command (assuming the calculation
was carried out for such a series by setting the appropriate parameter values
in the PARAMETER menu). Note that a MONTAGE will erase the screen before display,
regardless of the ERASE setting.
SET NOREQ-POS<>REQ-POS: When NOREQ_POS is set, individual images will
be written to the center of the display screen (assuming that NOMONTAGE is
set). When REQ_POS is set, the user will be prompted for the coordinates at
which the image is to be displayed.
NOMONT-SPACE<>MONTAGE-SPACE: is used to set the desired spacing between
the montaged images.
INT.AUTO-SCALE<>INT.ABS-SCALE: To see the most detail in any image,
set INT.AUTO-SCALE to display the image with its minimum set to black and
its maximum to white. To intercompare images, it is better to use INT.ABS-SCALE
to choose the same absolute scale for all the images.
CTF-AUTOSCALE<>CTF-ABS.SCALE: Can be used to scale a CTF plot by fixing
the maximum g value considered. In AUTOSCALE mode the CTF is drawn to where
it approaches zero.
PG-REC SP<>PG-REAL SP: determines whether or not the calculation is
done in reciprocal space or in real space. This switch should be set to reciprocal
space since the real space calculation is not debugged yet.
APERTURE<>NO-APERTURE: determines whether or not the current objective
aperture radius is drawn on a displayed diffraction pattern.
TITLES<>NO TITLES: determines whether titles are written under each
displayed image. Notice that MONTAGE will supress titles, but a title for
the montaged series may be added using WRITE TEXT.
2D-POT.SLICE<>3D-POT.SLICE: When the number of slices per unit cell
exceeds one in the MAIN menu, NCEMSS will sub-slice the unit cell in one of
two ways. When 2D-POT is set, the total potential within the cell will be
projected, and a portion assigned to each sub-slice. A more-accurate method
is to approximate the upper-layer zones by sub-slicing a three-dimensional
potential into the required number of sub-slices. In this way the variation
of the specimen structure in the electron beam direction is included in the
simulation. Of course, it takes longer in 3-D).
SET MIN. INTENSITY (LENS): sets the minimum diffracted beam intensity that
will be considered to pass through the objective lens; this minimum can be
set to exclude very low intensity beams from large defect unit cells, and
so speed up the image calculation.
SET MIN.INT.TO DISPLAY(FFT): determines down to what intensity diffracted
beams will be drawn in a diffraction pattern display.
SET CAMERA LENGTH: is used to adjust the magnification of the diffraction
pattern display. The value is input in mm., and has a default setting of 520mm.
INDEX DIFFR.PT.: is used to index a diffraction pattern. On moving the cursor
to the selected diffraction spot and clicking the mouse, the indices are written
next to the spot.
CHANGE CENTER OF DIFFR.PT.: The center of the displayed diffraction pattern
can be changed by selecting this command and using the mouse to click on the
desired position in the image display window.
READ THE CURSOR POSITION: reads the cursor position within an image.
ERASE THE DISPLAY: does just that.
WRITE TEXT ON THE DISPLAY: is used to write text at the cursor position.
STORE PARTS OF THE DISPLAY: after selecting this command, mark the corners
of an area of the display window (image) to be stored and the image will be
saved in a file. The user is prompted for a name and the program will automatically
add the extension .at
DISPLAY STORED IMAGE: use this command to displayed a stored image of the
type <name>.at created by the previous command.
PRINT STORED IMAGE FILE: sends the content of the file <name>.at to
a connected laserprinter. The program creates a file “laserprinter.ps” and
uses the command “lpr laserprinter.ps” to send the file to the printer. It
is up to the user to set up the appropriate redirection of the output to a
valid printer.
PRINT THE SCREEN: sends the content of the image window to a connected laserprinter.
It otherwise works identical to the command above.
LIST STORED IMAGE-FILES: sends the command “ls *.im” to the operating system.
The output list of stored image files is displayed in the terminal session
window.
SET CONTRAST FOR LASERWRITER: allows the user to change the values of brightness
(normally 0.5) and contrast (normally 1.0) of the printed image
SET DIV.ANGLE FOR DP: use this to change the size of the displayed diffraction
spots in case the size is not optimal for viewing.
IMAGE ONLY<>OVERLAY ATOMS: controls whether atom positions are overlayed
on the image or not.
AUTOSCALE-FIXED: use this to either let the computer choose black and white
levels automatically or to use fixed values input by the user.
DISPLAY<>PRINT: in the display position, anything “DISPLAYED” goes
to the image window. In the PRINT position, the actual numeric data is sent
to a file in a format that depends on the setting of the switch ascii/binary
below.
REL PHASE <> PHASE: determines if the phases reported for diffracted
beams include the phasechange due to the mean inner potential of the crystal
ASCII FILE<>BINARY FILE: determines if the numeric output data for
an image, projected potential or complex wavefunction is in ascii or binary.
OUT->PRINTER<>OUT->FILE: normally when you reroute the output
to the printer, the program executes the command “lpr laserprinter.ps”. Selecting
OUT->FILE will create a named postscript file that can be saved and printed
at any time later.
NORM.MONT<>CUSTOM: allows extra control on the layout of montaged
images.
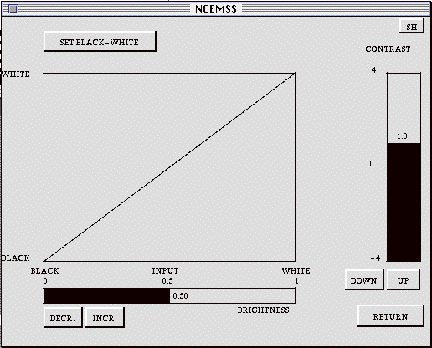
3.13 The SET-CONTRAST menu
When the ADJ.CNT box of the IMAGE-DISPLAY menu is activated, it brings up the SET-CONTRAST menu. This menu displays the current contrast and brightness settings graphically. The straight line shows the mapping of the image intensity values (horizontal axis) into the displayed output intensity values (vertical axis). For a one-to-one mapping, the values of contrast (vertical bar-graph) and brightness (horizontal bar-graph) should be 1.0 and 0.5 respectively.
To increase (or decrease) the contrast used to display the image, tap the
mouse with the cursor positioned over the UP (or DOWN) boxes underneath the
vertical bar-graph. The contrast-transfer graph will pivot about its mid-point
as the contrast is changed, providing a plot of how input grey levels are
mapped into output greyscale levels. Note that a contrast value of less than
zero will produce a negative image.
To increase (or decrease) the image brightness, use the INCR. and DECR.
boxes to move the mid-point of the contrast-transfer graph to the left or
right.
The contrast-transfer curve may be set directly, by activating the SET BLACK-WHITE
box, then clicking the mouse after positioning the cursor at one end-point
of the desired line, then clicking at the other endpoint. These end-points
need not be exactly on the lines forming the box enclosing the contrast-transfer
graph.
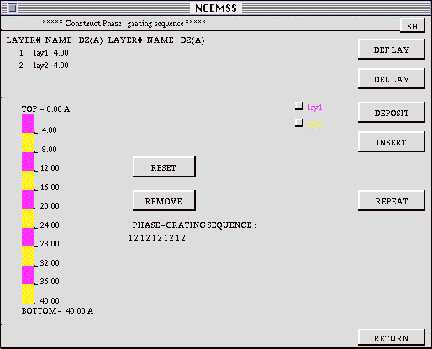
3.14 The SET-LAYERS menu
If the LAYERED STRUCTURE option is selected from the SINGLE/LAYERED menu, then the SET-LAYERS menu appears. This menu can be used to “construct” a specimen consisting of multiple layers of different single structures.
DEF LAY: To include a structure in the phase-grating sequence thatwill comprise
the final layered structure, use the DEF LAY box and enter the name of the
structure as it appears in the FILE-LIST menu (p.14). Up to six different
structures may be used to make up the layered structure. Note that a PHSGRT
calculation (p.21) must be carried out for any structure before it can be
included in a layered calculation. Also note that, as well as existing, all
the phase-gratings used to build a layered structure must be the same shape
and size; i.e. each phase-grating must have the same values for the projected
(two-dimensional) cell axes and cell angle, and also be computed out to the
same scattering parameter, GMAX.
DEL LAY: This box is used to remove a previously-defined layer name from
consideration.
DEPOSIT: The layered structure can be built up by depositing layers of any
member structure that was defined earlier using DEF LAY. Each deposition is
made by clicking on the DEPOSIT box, then on the appropriate LAYER symbol,
then entering the layer thickness desired. The final structure is built from
the top down; i.e. each subsequent layer is deposited onto the bottom of any
existing sequence. A graphical repesentation of the structure appears on
the left of the menu, and the phase-grating sequence is also listed.
INSERT: In addition to depositing a specified thickness of a chosen layer,
it is possible to insert a specified thickness at any chosen thickness of
the final structure. Clicking on this button, followed by the appropriate
LAYER symbol, causes NCEMSS to ask for a layer thickness to be inserted, and
the structure thickness at which to insert it.
REPEAT: This button is used to repeat a defined sequence a chosen number
of times in order to build up a periodic layer structure.
RESET: This button zeros everything in preparation for another try.
REMOVE: The phase-grating sequence can be operated on directly to remove
single slices, one at a time, by activating this button and clicking on the
offending phase-grating in the sequence.
Appendix A Multislice Size, PhaseGrating Size, and Maximum G
The “size” of a multislice calculation is defined conveniently by the size of the largest array (the Q(k) or q(x) array). For an array size of 2nx2m, the multislice is said to be a “parameter n+m” multislice; thus a parameter-16 multislice will have a Q(k) array size of 256x256, (or 512x128, or 1024x64, or 2048x32, or 4096x16, depending upon the shape of the unit cell used in the computation). This size parameter must apply to all multislice programs, regardless of which of the three current algorithms (reciprocal-space, Fourier-transform, or real-space) is employed by the program.
A.1 Reciprocal-space multislice
As introduced by Goodman and Moodie (1974), the basic recursive form of
the multislice description of dynamical diffraction can be written as
Yn+1(k) = [Yn(k) · Pn+1(k)] * Qn+1(k) (A1)
That is, Yn+1(k), the wave function (given in reciprocal space) at the exit
surface of the (n+1)th slice, is obtained by multiplying the wave function
at the exit surface of the nth slice by Pn+1(k), the propagator for the (n+1)th
slice, followed by the convolution of this result by Qn+1(k), the phase-grating
function (given in reciprocal space) for the (n+1)th slice.
In multislice computer programs that use the above reciprocal-space formulation,
the three functions, Y(k), P(k), and Q(k) are represented by two-dimensional
arrays containing terms with indices that can be regarded as those of the
diffracted beams within the diffracting specimen. In order to impose no extra
symmetry on the computation, a “circular aperture” is usually placed on the
terms in the arrays, so that terms beyond a certain distance in reciprocal
space are set to zero. Note that the Q(k) array must extend out to twice as
far in reciprocal space as the Y(k) and P(k) arrays in order to correctly
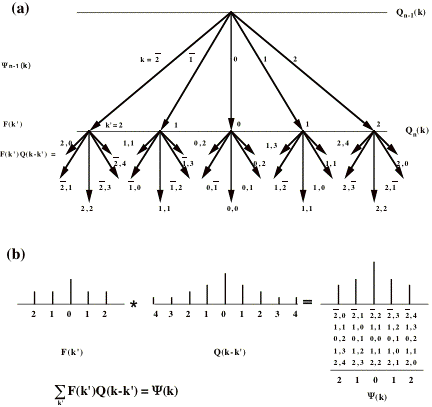
include all physical scatterings to each diffracted beam. Figure A1 shows
how this doubled phase-grating requirement arises because Q(k) is a “probability
map” of terms that determine how much of each diffracted beam is to be scattered
through the angle corresponding to the term. Thus, in order to compute the
scattering of diffracted beams out to k = (h,k), the Y(k) and P(k) must be
(2h+1)x(2k+1) in size, and Q(k) must be (4h+1)x(4k+1). For example, the SHRLI80
programs used a 128x128 array for Q(k), making SHRLI80 a parameter-14 multislice
and giving a maximum (h,k) value of (31,31); this limits the number of diffracted
beams to less than 4096, adequate for most perfect-crystal computations, but
too small for simulation of many defect structures (O’Keefe et al, 1978).
A.2 Fourier-transform Multislice
For larger arrays (and thus larger numbers of diffracted beams), it is faster
to compute the multislice by recasting (A1) into a form where the convolution
is replaced by two Fourier transforms and a multiply operation, as was done
by early users of multislice in the Melbourne group.
Then
Yn+1(k) = F [F -1[Yn(k) · Pn+1(k)] · qn+1(x) (A2)
Here the F represents the Fourier transform operation, and q(x) is the real-space
form of Q(k), i.e. the (inverse) Fourier transform of Q(k). Experience with
the SHRLI programs has produced the not-surprising result that, in order to
obtain the same results with (A2) as with (A1), q(x) must be formed from a
Q(k) that extends twice as far in reciprocal space as do Y(k) and P(k).
Note that, as well as correctly describing the physics of the scattering
process by ensuring that all contributions from all the diffracted beams leaving
the previous slice to each diffracted beam from the current slice are included,
the doubled phase-grating also neatly eliminates the possibility of any “aliasing”
arising from the necessary sampling of the real-space functions. Unfortunately,
in their description of the FFT multislice, Ishizuka and Uyeda (1977) stated
that the number of diffracted beams must be no less than the number of phase-grating
coefficients; under their condition, the effects of aliasing will produce
incorrect scattering results if array sizes are not made large enough to
produce essentially zero electron amplitude over the outer five-nineths of
the phase-grating and wave-amplitude arrays. This confusion appears to have
arisen when the concept of FFT multislice was introduced to the Kyoto group
by a visiting researcher familiar with its use in the Physics Department
of Melbourne University. At Melbourne, it had been found that aliasing occurred
when the convolution step of the reciprocal-space multislice (equation A1)
was replaced by a forward/inverse Fourier transform sequence. This aliasing
boosted the amplitudes of the outer beams in the calculation until “knock
off” parameters were introduced to set the outer beam amplitudes to zero
after each slice. However, even after this procedure eliminated the aliasing
effect, results from the FFT multislice did not exactly match ones from the
“standard” reciprocal-space formulation (O’Keefe, 1972). For this reason,
the SHRLI80 programs (O’Keefe et al, 1978) continued to use the (slower)
reciprocal-space form of the multislice. Experiments with various scattering
algorithms (Self et al, 1983) led to the testing of different ways of avoiding
aliasing in FFT multislice. It was realized that one such method was by choosing
a q(x) formed from Q(k) terms that extended only 2/3 of the way to the array
edges, provided that only the same number of diffracted beams was used in
Y(k), with the outer 5/9 of the diffracted beam array reset to zero after
every slice. A better method was to ensure that q(x) was formed from a Q(k)
that extended out to twice the scattering angle as Y(k), and to reset the
outer 3/4 diffracted beams to zero after each slice. This latter method conforms
to the physics of the scattering process (fig.A1), and proved to yield the
same results as the reciprocal-space multislice. A multislice program using
this method was incorporated into the SHRLI81 suite, and this method is used
in the NCEMSS multislice program (Kilaas, 1987).
A.3 Real-space multislice
A third method of computing the multislice is to carry out the calculation completely in real space; this is an alternative to computing in reciprocal-space (as in equation A1), or in both real and reciprocal-space (as in equation A2). Fourier transformation of (A1) gives
yn+1(x) = [ yn(x) * pn+1(x) ] · qn+1(x) (A3)
In this formulation the real-space wave function yn(x) is convolved by a
real-space propagator pn+1(x) and the result multiplied by the real-space
phase-grating. Van Dyck (1983) has developed this method and shown that the
convolution step need not be carried out with the full 2nx2m p(x) array, but
only with a such smaller array (since p(x) is sharply peaked in the forward
direction for high energy scattering). Since the modified p(x) array is so
much smaller, the computation time should take less time than either of the
reciprocal-space multislice (A1) or the FFT multislice (A2); however, tests
(e.g. Kilaas and Gronsky, 1983) have shown that the original formulation of
the method required more beams and smaller slices to achieve the same precision
as either the reciprocal-space multislice or the FFT multislice, resulting
in a longer time to produce the wavefield at the same total specimen thickness.
Van Dyck and Coene (1984) have since proposed a modified implementation of
the real-space multislice into a workable algorithm, with results that approach
those produced by the multislice formulations of equations A1 and A2 (Coene
and Van Dyck, 1984). Since the p(x) array is much smaller, procedure (A3)
does produce some saving in memory over the other multislice formulations.
All three formulations of the multislice procedure require the computer (or array processor) to store three different complex arrays corresponding to the phasegrating function in real or reciprocal space (q(x) or Q(k)), the electron wavefield in real or reciprocal space (y(x) or Y(k)), and the propagator function in real or reciprocal space (p(x) or P(k)).
With a reciprocal-space phasegrating Q(k), of 2nx2m terms, a parameter-(n+m)
reciprocal-space multislice (equation A1), requires a reciprocal-space wavefield
array (or set of diffracted beams), Y(k), of 2n-1x2m-1 terms, and a reciprocal-space
propagator array P(k), of 2n-1x2m-1 terms.
An equivalent parameter-(n+m) FFT multislice (equation A2) requires a real-space
phase-grating array q(x), of 2nx2m terms, an electron wavefield array Y(k),
of 2nx2m terms, and a reciprocal-space propagator array P(k), of 2n-1x2m-1
terms.
For a real-space parameter-(n+m) multislice (equation A3), both the y(x)
and q(x) arrays need to hold 2nx2m terms, whereas p(x) may be as small as
thirteen (Kilaas & Gronsky, 1983), giving a total requirement of slightly
over 2x2n+m terms. In implementing the real-space multislice it is important
that the 2nx2m q(x) array should be formed from a full 2nx2m Q(k) terms, whereas
the 2nx2m y(x) array should be formed from only 2n-1 x2m-1 Y(k) terms in
order to include correctly all the physical scattering contributions to each
diffracted beam and to avoid aliasing problems (fig A1).
Any (correctly implemented) multislice of size 2nx2m (parameter n+m) thus
includes the effects of only 2n-1x2m-1 diffracted beams. This is true for
all three formulations of the multislice: the reciprocal-space method (equation
A1), the FFT method (equation A2), and the real-space multislice (equation
A3).
�
Coene W, Van Dyck D (1984) The real space method for dynamical electron diffraction calculations in high resolution electron microscopy. II. Critical analysis of the dependency of the input parameters. Ultramicroscopy 15, 41-50.
Goodman P, Moodie AF (1974) Numerical evaluation of N-beam wave functions
in electron scattering by the multislice method. Acta Cryst. A30, 322-324.
Kilaas R, Gronsky R (1983) Real space image simulation in high resolution
electron microscopy. Ultramicroscopy 11, 289-298.
Kilaas R (1987) Interactive software for simulation of high resolution TEM
images, Proc. 22nd MAS, R. H. Geiss (ed.), Kona, Hawaii, 293-300.
and Kilaas R (1987) Interactive simulation of high resolution electron micrographs.
In 45th Ann. Proc. EMSA, G.W. Bailey (ed.), Baltimore, Maryland,
66-69.
Ishizuka K, Uyeda N (1977) A new theoretical and practical approach to the
multislice method. Acta Cryst. A33, 740-749.
O’Keefe MA (1972) Lattice images of large-unit-cell oxide crystals by n-beam
theory. M.Sc thesis, University of Melbourne.
O’Keefe MA, Buseck PR, Iijima S (1978) Computed crystal structure images
for high resolution electron microscopy. Nature 274, 322-324.
Kilaas R. (1987) Interactive software for simulation of high resolution
TEM images, Proc. 22nd MAS, R. H. Geiss (ed.), Kona, Hawaii, 293-300.
Kilaas R. (1987) Interactive simulation of high resolution electron micrographs.
In 45th Ann. Proc. EMSA, G.W. Bailey (ed.), Baltimore, Maryland,
66-69.
O’Keefe MA, Kilaas R (1988) Advances in high-resolution image simulation.
Scanning Microscopy Supplement 2, 225-244.
Self PG, O’Keefe MA, Buseck PR, Spargo AEC (1983) Practical computation
of amplitudes and phases in electron diffraction. Ultramicroscopy 11, 35-52.
Van Dyck D (1983) High-speed computation techniques for the simulation of
high resolution electron micrographs. J. Microscopy 132, 31-42.
Van Dyck D, Coene W (1984) The real space method for dynamical electron
diffraction calculations in high resolution electron microscopy. I. Principles
of the method. Ultramicroscopy 15, 29-40.
Appendix B HOLZ interactions
With suitable algorithms, it is possible to include in the diffraction calculation the effects of out-of-zone scatterings, or non-zero (or higher-order) Laue zone (HOLZ) interactions. Basically, there are four ways to produce the set of phasegratings (or projected potentials) that describe the “multisliced” crystal. For structures with short repeat distances in the beam direction, the simplest method is to use one slice per unit cell. For structures with large repeats in the beam direction, several methods may be used, three of which rely on sub-dividing the slice into “sub-slices”. Any of the four methods can be used in NCEMSS.
B.1 Identical slices with only one sub-slice per unit cell repeat distance
A multislice computation in which every slice is identical contains no information about the variation in structure along the incident beam direction, and includes scattering interactions with only the zero-order Laue zone (ZOLZ) layers. For structures with short repeat distances in the beam direction such a computation is adequate, since the Ewald sphere will not approach the (relatively distant) high-order zones.
B.2 Identical sub-slices with n sub-slices per unit cell repeat distance
For structures with large repeats in the beam direction, a method of sub-dividing the slice is required in order to compute the electron scattering with sufficient accuracy. The simplest, but most approximate method, is to compute the projected potential for the full repeat period then use 1/n of the projected potential to form a phase-grating function that can be applied n times to complete the slice. This method avoids interaction with any “pseudo-upper-layer-line” (Goodman and Moodie, 1974), but ignores real HOLZ layers.
B.3 Sub-slices based on atom positions
An improvement on sub-dividing the projected potential is to sub-divide the unit cell atom positions. In this procedure the list of atom positions within the unit cell is divided into n groups depending upon the atom position in the incident beam direction. From these sub-sliced groups, different projected potentials are produced to form n different phase-gratings, which are applied successively to produce the scattering from the full slice.
B.4 Sub-slices based on the three-dimensional potential
A further improvement on sub-dividing the atom positions, is to sub-divide the three-dimensional potential of the full slice, since an atom with a position within one sub-slice can have a potential field that extends into the next sub-slice. Rather than compute a full three-dimensional potential and then integrate over appropriate sub-slices (a 128x128x128 potential would require over two million samples to be stored), it is possible to derive an analytical expression for the potential within the sub-slice z0 Dz projected onto the plane at z0 (Self et al., 1983). It is possible to apply this method routinely to structures with large repeats in the beam direction, thus generating several different phase-gratings for successive application, and even to structures (perhaps with defects) that are aperiodic in the beam direction and require a large number of individual non-repeating phase-gratings (Kilaas et al., 1987).
B.5 NCEMSS sub-slicing
While ensuring that the calculation remains sufficiently accurate, NCEMSS will normally choose the simplest (and quickest) method of specifying how slices are defined for any particular combination of specimen, zone axis, accelerating voltage, and maximum g. To this end, the user can choose to neglect HOLZ interactions if these are judged to be unimportant. If HOLZ interactions are important, then the user should select the “3D-POT.SLICE” box in the SET-UP menu (p 41), rather than the “2D-POT.SLICE” box.
When a two-dimensional calculation is selected, NCEMSS will use one slice
per cell if the cell repeat distance in the beam direction is small (B.1).
If the repeat distance is too large for one slice per unit cell, NCEMSS will
avoid pseudo-upper-layer-lines by producing n identical sub-slices (B.2).
When a three-dimensional calculation is selected, (3D-POT.SLICE activated),
NCEMSS uses a sub-divided three-dimensional potential (B.4) when the repeat
distance is large, and defaults to one slice per cell if the distance is small
enough. Note that the number of sub-slices per unit cell can be forced to
be greater than one by setting it explicitly in the MAIN menu (p 16); this
will ensure that any HOLZ interactions are included even for small repeat
distances. Of course, if the repeat distance is very small, leading to a distant
HOLZ in reciprocal space, both the calculation and the experiment it is modeling
will interact only very weakly with the HOLZ reflections.
Use of the LAYERED STRUCTURE option (p 12) to produce the scattering from
a structure that is layered or aperiodic in the incident beam direction is
effectively an application of the method of sub-slicing based on atom positions
(B.3). Thus the user could create a number of sub-slices by assigning selected
atoms to different structure files, then forming a phasegrating for each sub-slice,
and using the SET-LAYERS menu (p 46) to specify how the sub-slices are to
be used to describe the specimen structure. Normally, of course, the use
of the B.4 option is to be preferred, as it produces a superior result, and
is far easier to use.
B.6 Other methods
Van Dyck has proposed other methods to include the effects of HOLZ layers,
including the second-order multislice with potential eccentricity (Van Dyck,
1980) and the improved phase-grating method (Van Dyck, 1983). Tests of these
procedures show that the extra computation involved in using potential eccentricity
may be worthwhile, but that the improved phase-grating method diverges too
easily to be useful.
Goodman P, Moodie AF (1974) Numerical evaluation of N-beam wave functions
in electron scattering by the multislice method. Acta Cryst. A30, 322-324.
Kilaas R, O’Keefe MA, Krishnan KM (1987) On the inclusion of upper Laue
layers in computational methods in high resolution transmission electron
microscopy. Ultramicroscopy 21, 47-62.
Self PG, O’Keefe MA, Buseck PR, Spargo AEC (1983) Practical computation
of amplitudes and phases in electron diffraction. Ultramicroscopy 11, 35-52.
Van Dyck D (1980) Fast computational procedures for the simulation of structure
images in complex or disordered crystals: A new approach. J. Microscopy 119,
141-152.
Van Dyck D (1983) High-speed computation techniques for the simulation of
high resolution electron micrographs. J. Microscopy 132, 31-42.